Exploring the Microbial Diversity in Biological Soil Crusts at Joshua Tree National Park

Nuttapon Pombubpa¹, Tania Kurbessoian¹, Jason E. Stajich¹, ² Nicole Pietrasiak, ³Tasha La Doux

¹ Department of Microbiology & Plant Pathology and Institute of Integrative Genome Biology, University of California, Riverside, Riverside, California 92521, USA

² Plant and Environmental Sciences Department, New Mexico State University, Las Cruces, NM 88003, USA

³ Sweeney Granite Mountains Desert Research Center, University of California, Riverside, Kelso, CA 92309, USA

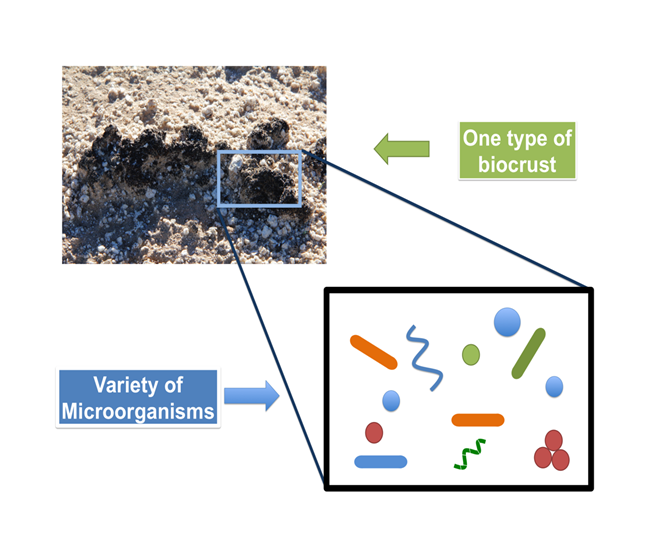
Figure 1. Biocrusts are like a “living skin” on top of arid landssoil. They consist of a living community of microorganisms such as bryophytes, lichens, eukaryotic algae, cyanobacteria, bacteria, and fungi. These complex communities contribute to healthy desert ecosystems by promoting nutrient cycling and reducing soil erosion.

Introduction

Up to 40% of the global land surface consists of desert environments (also known as dryland regions, semi-arid and arid lands) (Belnap et al. 2016). Due to the sparse water availability, deserts are typically devoid of dense vegetation and the spaces between plants may appear barren at first glance. These plant interspaces, however, are often occupied by a microscopic world forming soil surface structures recognized as “biological soil crusts (or biocrusts)” (Belnap et al. 2001). These biocrusts form at the uppermost millimeters to centimeters of soil and are an aggregation of minerals and microorganisms. In dryland regions, biocrusts can cover up to 70% of the land surface area (Belnap et al. 2016), including the desert floor of Joshua Tree National Park (JTNP). Within biocrust, a huge variety of microorganisms can coexist and cooperate as a community. For example, biocrusts can be made up of bryophytes, lichens, eukaryotic algae, cyanobacteria, bacteria, and fungi, which all interact cooperatively to create a protective and productive community on the soil surface (Figure 1) (Belnap et al. 2001, Belnap et al. 2016). Forming a hot zone of biodiversity at the soil surface, biocrust can be thought of as a “living skin” on top of the soil, where each microbial member is an essential contributor to the ecology of desert environments (Belnap et al. 2016).

Biocrusts play important roles in desert ecosystems. For instance, they facilitate carbon and nitrogen cycling through biochemical processing performed by the microorganisms that inhabit the crusts. They contribute to effective soil nutrient cycles, prevent soil erosion, improve regeneration, and stabilization of vegetation, therefore creating a healthy and stable ecosystem (Belnap and Gardner 1993, Belnap et al. 2001, Belnap et al. 2016, Weber et al. 2016). To better understand these complex microbial communities, studies of microorganisms that inhabit and enable the functions of biocrusts are needed.

The goals of this article are threefold: 1) to provide a basic understanding of biocrusts and the microbial diversity found within them; 2) to summarize the findings from previous research conducted in JTNP by a team of scientists over the last two decades and 3) to build upon that knowledge base by presenting additional data collected by the authors of this paper. More specifically, we developed protocols that further investigate the microbial components found in the biocrusts at JTNP such as algae, bacteria, and especially fungi, as this was one of the major knowledge gaps regarding microbial diversity in the park.

Figure 2. Light algal crusts (LAC) are the most common biocrust types in JTNP. They are dominated by cyanobacteria and other algae that quickly turn green once water is added; within 24 hours the algae and cyanobacteria become active (far right), but without the water are invisible to the naked eye (far left).

Biocrusts at JTNP

Within the hot Mojave and Sonoran desert biomes, including the area of JTNP, biocrusts can be hard for the untrained eye to notice. These cryptic communities may appear to be bare unconsolidated soil, as they are generally difficult to identify from a distance. However, if we take a minute and look closer at the ground, biocrusts are frequently encountered, especially in the park. A hand lens or magnifying glass can reveal the telltale microscopic structures that are distinctive for many types of biocrusts (Figure 2). First, one will notice the consolidated nature of the crust aggregate that will hold the soil together cohesively as shown in Figure 2A. Biocrusts are also characterized by dangling filamentous components that can be seen among the subsurface of biocrust (Figure 2A). Those “danglies” represent biological filaments of cyanobacteria, or fungi that can appear like micro-roots; they are often seen with a few soil particles adhering to them.

Figure 3. Plant interspaces in JTNP contain a variety of biocrusts but are dominated by light algal crusts and lichen crusts, both of which will have characteristic filaments in the subsurface. The filaments look like tiny roots dangling from under the crust (A). Light algal crusts (A) and lichen crusts (B, C) are commonly found in JTNP. The majority of lichen crusts in JTNP are composed of two different fungal species: Collema coccophorum (B), which is a cyano-lichen crust and Clavascidium lacinulatum (C), which is a green algal lichen crust.

Biocrusts can be classified based on the dominant photosynthetic microorganisms present in the crust, which are the components that can perform photosynthesis just like plants fixing carbon dioxide from the atmosphere and producing oxygen. Photosynthetic microorganisms include cyanobacteria, other algae, lichens, liverworts or mosses (Pietrasiak et al. 2013). Light algal crusts (LAC) are the most common biocrust types in hot desert ecosystems, including the Mojave and Colorado Deserts at JTNP, and are dominated by cyanobacteria and other algae that quickly turn green in the presence of water (Figure 3; Pietrasiak et al. 2011a,b). Another type of biocrust is referred to as lichen crusts (Figure 2B), these consist of fungal and algal/cyanobacterial components. A lichen crust may have multiple species of lichen-forming or lichen associated fungi co-occurring within one crust structure (Figure 2B and 2C). Lichen crusts can also be found throughout the desert Southwest, but have a more patchy distribution, particularly in JTNP (Pietrasiak et al. 2013). Two primary types of lichen biocrusts are found in JTNP: 1) a fungus with a cyanobacterial partner (Cyano-Lichen Crusts; CLC) or 2) a fungus with a green algal partner (Green Algal Lichen Crusts; GLC). Finally, moss dominated crusts are much more limited on the landscape, especially in JTNP. They occur preferentially in moist microhabitats, such as under the protective rock ledge of a boulder or along the shady banks of a riparian corridor; anywhere that moisture drips or runs off hard surfaces and can be trapped for longer periods (Pietrasiak et al. 2011a,b).

Algal and Cyanobacterial Diversity in Biocrusts

Most biocrust communities have a basic architecture that includes two main structural components: 1) primary producers that perform photosynthesis, and therefore produce carbohydrates and oxygen; and 2) associated heterotrophic consumers such as fungi and microscopic animals, which then live off the carbon-rich products that the primary producers generate. In JTNP, the most common primary producers in biocrust are cyanobacteria and other algae (Figure 3). These algae are making up the majority of the photosynthetic component in the LAC found throughout the park (Flechtner et al. 2013, Pietrasiak et al. 2011a,b, 2013). Under certain conditions microalgae may partner with fungi or mosses to create more complex biocrust communities such as lichen or moss crusts

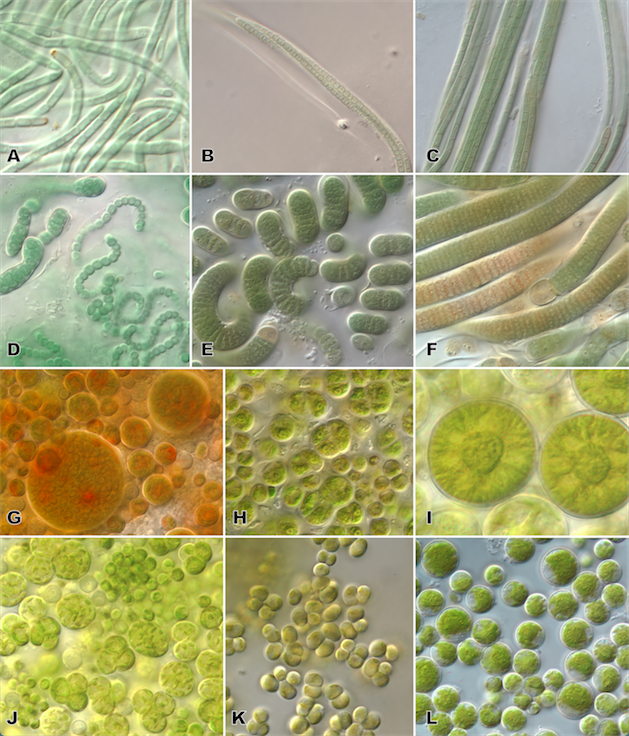
Figure 4. Cyanobacterial (A-F) and eukaryotic algal (G-L) diversity of cultures isolated from JTNP biocrusts. Photographs show: A) Oculatella coburnii (Synechococcales clade), B) Trichocoleus desertorum (Synechococcales clade), C) Symplocastrum flechtnerae (Oscillatoriales clade), D) Nostoc sp. (Nostocales clade), E) Spirirestis rafaelensis (Nostocales clade), F) Hassallia sp. (Nostocales clade), G) Bracteacoccus sp., H) Chlorosarcinopsis sp., I) cf Actinochloris sp., J) Myrmecia sp., K) Stichococcus sp., and L) Parietochloris sp.

Algae are very interesting organisms. The term “algae” refers to a very diverse group of organisms spanning across the entire tree of life, including members from the Prokaryotes (Kingdom: Monera) and Eukaryotes (Kingdom: Protista). While “algae” does not represent a technical taxonomic term and there is no agreed upon definition of what most people think of as “algae,” it generally refers to organisms that can photosynthesize, but aren’t plants. Examples of “algae” include groups of organisms like diatoms, green algae, yellow algae, and blue green algae also known as cyanobacteria (Figure 4). The latter are the only Prokaryotes (Bacteria) that photosynthesize. Each of these groups of algae represents their own lineage in the tree of life and they differ in cell organization and structure, pigmentation, and ecosystem roles. What unites the groups is the presence of the green pigment chlorophyll in their cells which enables the ability to perform photosynthesis while producing oxygen, and the lack of the reproductive organs and vegetative tissues found in multicellular plants (Graham et al. 2009).

Cyanobacteria are one group of algae that are extremely abundant in desert soils. They represent the majority of photosynthetically active biomass in biocrusts. These bacteria play essential roles in the desert environment. For example, cyanobacteria are adept at excreting sugary polymeric compounds around their cells that are very sticky and function as fibrous glue holding soil grains in place (Belnap and Gardner 1993). This sticky glue is very important in desert interspaces, where plants are lacking and only a few roots are available to stabilize the seemingly bare soil. The aggregation of soil enabled by the cyanobacteria helps reduce erosion. The stickiness of these cyanobacteria also traps dust, which often contains essential micronutrients that can be incorporated into to the soil (Belnap and Gardner 1993, Hu et al. 2002). Another important function performed by cyanobacteria is called nitrogen fixation, which brings substantial amounts of nitrogen into the nutrient poor desert soil (Belnap 2002, Pietrasiak et al. 2013). Through biochemical reactions performed by cyanobacteria, inert atmospheric nitrogen is incorporated into specialized cell compartments or cell types, where it is assimilated into organic molecules through a process called biological nitrogen fixation. Through these actions cyanobacteria enrich the desert topsoil with essential nutrients and help create a thin, fertile, and biologically active skin of the desert that we call biocrust.

Previous research has laid the foundation for the importance of cyanobacteria in desert soils, but we only have scratched the surface in understanding the breadth of species diversity. Prior studies on the diversity of cyanobacteria in JTNP have discovered many new species (Řeháková et al. 2007, Mühlsteinová et al. 2014, Osorio-Santos et al. 2014, Pietrasiak et al. 2014, Bohunická et al. 2015). Within the last 11 years a team of phycologists under the supervision of Jeffrey Johansen (John Carroll University, OH) and Nicole Pietrasiak (New Mexico State University, NM) described and published two new cyanobacterial genera (Mojavia, Roholtiella) and 5 new species (Mojavia pulchra, Roholtiella mohaviensis, Oculatella coburnii, Trichocoleus desertorum, Symplocastrum flechtnerae) from JTNP soils (Figure 4) using culture dependent methods. Additional assessment of the biocrusts of JTNP, among other desert systems, will certainly be needed to describe all the cyanobacterial members present in desert systems. The application of culture independent assessment using DNA-based description of biodiversity is likely to uncover additional genera and certainly new species of cyanobacteria in JTNP biocrusts. This discovery of taxa then opens the door to unraveling the various functions contributed to the ecosystem by these microorganisms.

Very little is known about the biodiversity of eukaryotic algae, including diatoms, green algae, and yellow algae in biocrusts, not to mention the ecosystem roles of these organisms. The few studies that have been done on eukaryotic algae in biocrust, indicate that the contribution of these groups of algae to biomass is rather low but their diversity is much greater than in cyanobacteria (Büdel et al. 2016). To date, the only published study investigating the eukaryotic algal diversity of JTNP used a culture dependent approach (Flechtner et al. 2013). In this study, the authors isolated living algal strains by placing soil on culture medium and observing and isolating the organisms which grew. The authors intensively studied 95 algal isolates from 18 locations within JTNP using morphological observations and DNA sequence information from these isolates. This study revealed 28 unique lineages in the families of Chlorophyceae (17), Trebouxiophyceae (7), Xanthophyceae (3) and Eustigmatophyceae (1). Most did not match any described algal species in published taxonomic keys, highlighting the poor knowledge we currently have about these organisms, but more importantly, and their great potential for discovery of new species (unknown to science). In the same year, Fučíková et al. (2013) included selected JTNP algal isolates in an extensive revision of the green algal genus Bracteacoccus and newly described 5 Bracteacoccus species from dryland environments. This monographs reports several records of Bracteacoccus species from JTNP including: 4 records of the established Bracteacoccus pseudominor found at 3 locations within the Colorado desert portion of the park, 1 record of the newly described Bracteacoccus deserticola from the Pinto Basin, 1 record of the newly described Bracteacoccus glacialis found in the Wonderland of Rocks, and 9 records of the newly described Bracteacoccus occidentalis from 5 locations within JTNP. In 2014, a new genus and species of green algae, Rotundella rotunda, was discovered on the alluvial fans near Eagle Mountain and named by Fučíková et al. (2014). Many more discoveries of enigmatic algae from biocrusts can be anticipated in the future

Fungi Diversity in Biocrusts

Studies of biocrusts have primarily focused on algal and bacterial communities as part of understanding the microbiological composition of crusts classified by morphology. Exploration of the fungi in the biocrust systems is still an emerging research area and is needed to better understand
the functional roles they play in the morphological properties and nutrient cycling activities of soil surfaces (Maier et al. 2016, Maier et al. 2018). Currently there are limited published reports on fungal diversity in biocrusts and no previous fungal study in biocrust has been done at JTNP. Most studies were conducted with culture dependent approaches, which underestimate microbial diversity. One study examined fungi in crusts using denaturing gradient gel electrophoresis (DGGE) (Bates and Garcia-Pichel 2009), which is used as a fingerprinting method to estimate environmental microbial diversity. DGGE has only limited utility as it does not allow direct identification of species, only a pattern of sizes of DNA bands run on a gel that can be matched between sample sites to look for similarities. To overcome this, DNA sequence based approaches are applied to estimate diversity and identify fungal species directly from environmental samples of biocrusts (Steven et al. 2014, Steven et al. 2015, Maier et al. 2018).

Figure 5. Serial dilution method involves a dilution series of biocrust water suspensions are prepared by adding biocrust to 100 ul of sterile water. To dilute the biocrust water suspension, 10 ul of original solution is transferred and combined with 90 ul of sterile water (1:10 dilution). Additional dilutions are created by repeating this step: 1:100 and 1:1000, accordingly.

Mechanisms for discovering microorganisms

Technology advances have enabled and simplified sampling methods for DNA sequencing that allow us to explore microbial diversity found in nature, very little research has focused on conducting inventory type studies of biocrust. There are two ways to assess the biological diversity found within a biocrust. The first approach, called “culture dependent,” results from using cultured strains of organisms that were present in the soil sample. This is achieved by plating biocrust soils onto semi-solid microbiological media in order to further isolate life strains and eventually obtain individual isolates of each taxonomic entity. The media consists of nutrients for the organisms to grow and agar to provide a surface to visualize and observe morphologies of the isolates. The nutrient content of the media can be adjusted to favor the growth of one microorganism over another. Specifically, a serial dilution is used to isolate the microbes from the soil (Figure 5). This method involves making a soil slurry by suspending the soil sample with increasingly higher proportions of water or media, in order to get a low starting concentration of spores and reduce to manageable counts the number of species growing on the Petri dishes. In order to isolate single organisms, 100 uL of biocrust-water suspensions are spread on a variety of media and the growth of microbial colonies is scored over the course of a few days. An alternative method used with the serial dilutions is called pour plating, where the crust-water solution can be poured to differentiate among microorganisms based on their oxygen dependence. The top layer obviously favors oxygen-loving microbes, whereas the bottom layer, which is submerged in water, selects for oxygen sensitive strains (Clark 1967). Once axenic cultures have been obtained, DNA sequence information can be generated directly from isolated microorganisms from this culture dependent method.

Although microbial diversity in biocrust can be explored to some extent using a culture dependent method, basic growth media may not provide suitable conditions for the growth of the majority of microorganisms. Direct DNA sequencing from soil samples can be used to capture greater microbial diversity and represent a “culture independent” method for assessing biocrust microbial communities. These molecular and genomic technologies are contributing tremendously to achieve a better understanding of the microbial diversity and composition of many environments from the human body to the open ocean. PCR amplification and Next Generation Sequencing (NGS), are used to assay regions of the genome which are found in all organisms. One of these, the 16S ribosomal RNA (rRNA) gene is used to survey Bacteria and Archaea while the Internal Transcribed Spacer (ITS) regions can be used to identify fungi present in a sample. These molecular markers have proven successful in recovering a broad range of bacterial and fungal diversity in soil microorganisms (Caporaso et al. 2012, Smith and Peay 2014). Broad sampling and fine scale analysis with NGS can be used to effectively compare biodiversity among biocrusts from different locations or classified as different morphological types. These studies can help identify the core taxonomic composition of biocrusts and indicate key organisms that may play important roles in the formation and ecological functions of biocrust.

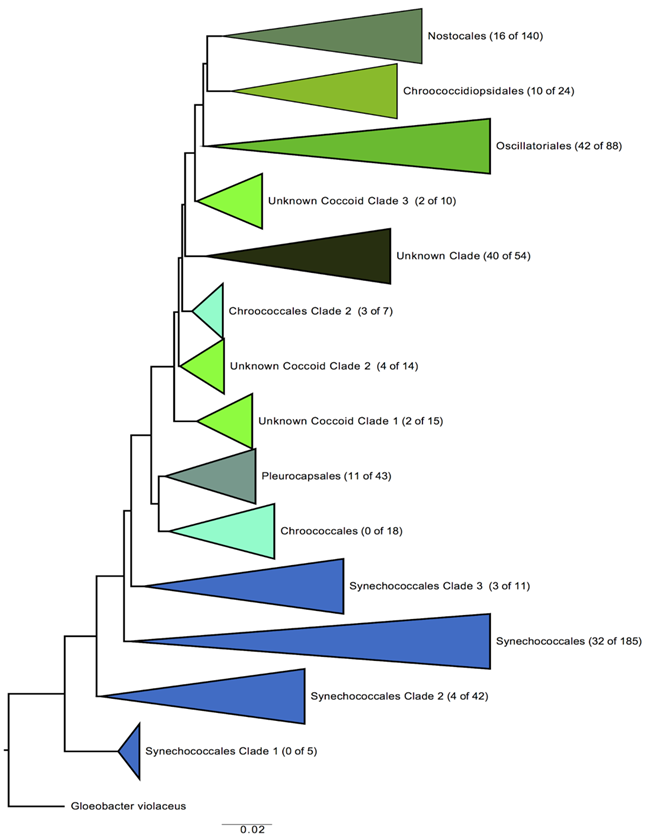
Figure 6. Phylogenetic tree of Cyanobacteria with all major clades shown. The number of lineages found in JTNP biocrusts out of the total number of known lineages is shown in parentheses to the right of the clade. These data are based on amplicon sequences and they illustrate that members of nearly all (12 of 14) of the major terrestrial cyanobacteria clades have been recovered from biocrusts in JTNP.

Current Research Results

We have used NGS sequencing (amplicon sequencing) of the 16S gene on collections we made of LAC and CLC biocrusts in Joshua Tree National Park to test whether there are differences in species that comprise these crust types. DNA samples from both crust samples were extracted, amplified with Polymerase Chain Reaction (PCR) targeting the 16S gene marker and sequenced using Illumina MiSeq. This sequencing captured a broad range of bacterial diversity and using bioinformatics analyses we focused first on the observed diversity of Cyanobacteria. Comparing these sequences with a collection of previously generated sequences from Cyanobacteria cultures compiled by Drs. Johansen and Pietrasiak, we constructed a phylogenetic tree representing the diversity of the JTNP cyanobacteria (Figure 6). Our analysis found that Cyanobacteria from nearly all known described groups (major clades) are present in the biocrust samples. Our work also demonstrates that both culture dependent and culture independent methods can equally recover the broad phylogenetic diversity found in biocrusts for Cyanobacteria (Figure 6). Further work on additional groups of Bacteria will help determine the extent of novel taxa which can be observed from the culture independent methods.

We have also assessed the composition of fungal communities using amplicon sequencing of biocrust DNA. The Internal Transcribed Spacer (ITS) 1 ribosomal gene region was amplified with PCR to inventory the fungi present in the biocrust samples using primers (Smith and Peay 2014) that are also being used to identify fungi in the Earth Microbiome Project (Walters et al. 2016). The PCR products are sequenced on an Illumina MiSeq to produce sequence fragments ~300 bp long. The DNA sequence fragments are compared to each other to collect them into groups which all represent sequences that are mutually similar based on the percentage of DNA bases that match. These clusters of sequences represent a guess of a fungal species or strain that is present in the biocrust sample. To determine what might be the name of this fungus, the sequence is matched against a database of known sequences. A curated database called UNITE is one of the best references for fungi and contains an enormous library of fungal ITS sequences and corresponding species name (Nilsson et al. 2015).

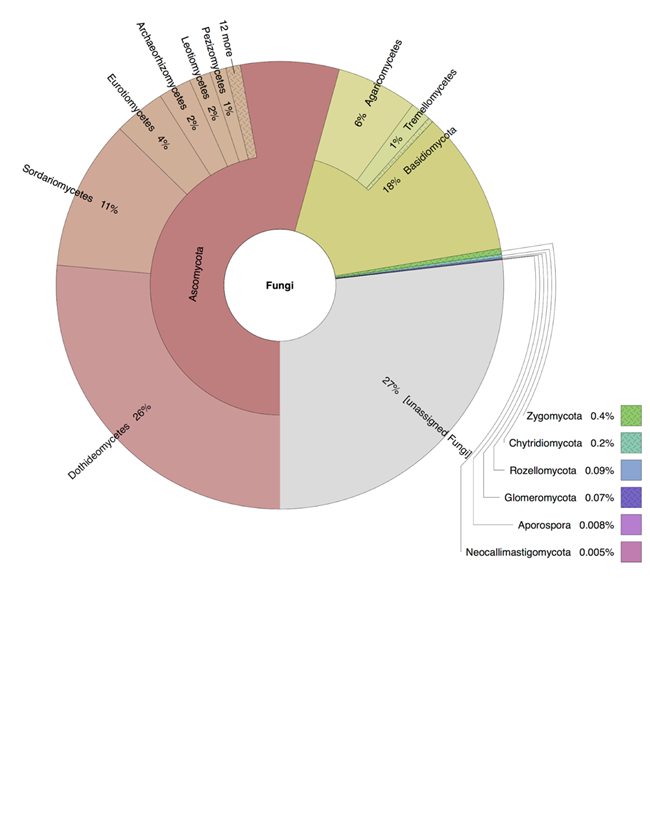
Figure 7. Fungal diversity in light algal crust from Joshua Tree National Park. Using Krona for visualization (Ondov et al. 2011), main fungal phyla are Ascomycota and Basidiomycota.

The ITS rDNA marker is sometimes referred to as a “barcode” as the sequence is often different between closely related species so that each species can have its own nearly unique signature. However, there can still be challenges with the marker as it still may be invariant among some groups of species. It is also difficult to use ITS sequences when they do not match any known Fungi, as it can be difficult to guess if it is a new species or species group not previously seen before. As we have seen in this and many other studies of fungi from the environment, there is vast, unsampled biodiversity that is only now being revealed through amplicon sequencing which leads to many sequenced ITS sequences assigned as an Unknown Fungus.

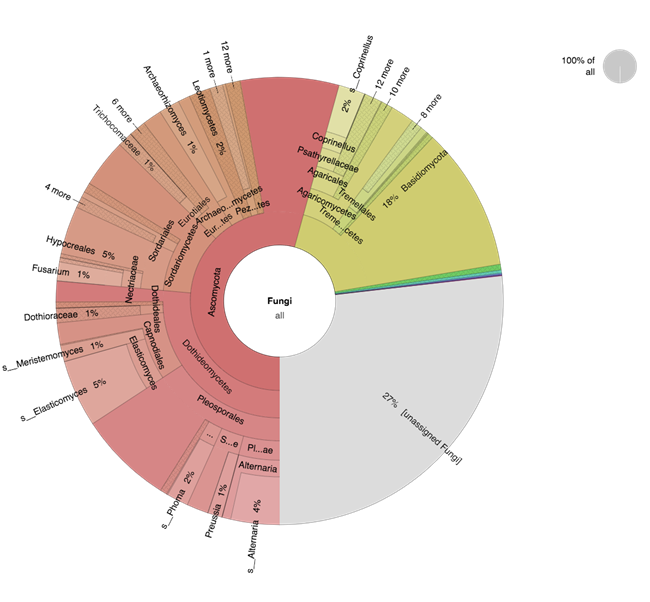
Figure 8. Light algal crust (LAC) from Joshua Tree National Park contains a complex fungal composition. A variety of fungal species are represented with several dominant species from Basidiomycota (yellow) and Ascomycota (red).

Analysis of our samples identified that biocrusts of different morphological classifications (e.g. LAC and CLC) are comprised of varied fungal taxa that differ at the genera and family level but are fairly consistent when comparing the presence of major phyla. The observed groups that dominate the crusts include Dothideomycetes, Eurotiomycetes, and Sordariomycetes within the Ascomycota and Agaricomycetes and Tremellomycetes from the Basidiomycota (Figure 7). These results are similar to previously reported types of fungi found in biocrusts using other methods (Bates and Garcia-Pichel 2009 and Steven et al. 2015). Within the light algal crust (LAC), the three most abundant Ascomycota genera were Alternaria, Phoma, and Elasticomyces; whereas, the top three fungal genera from Basidiomycota were Coprinellus, Cryptococcus, and Clitopilus. While mushrooms do inhabit some arid regions, we did not observe any fruiting in the regions where we sampled and were surprised to see the high abundance of some of these basidiomycetes. It may be that taxa are from spores that have blown in and are dormant awaiting a rain event. Our efforts have provided a high-resolution look at the fungal taxa that can be present in biocrusts and one arid region. The species reported from our study are only examples of some of the most abundant types of fungi living in biocrusts. We expect that many more fungi contribute to the biocrust community (Figure 8), but to identify the less abundant species will be undertaken with additional sequencing and robust analyses to confirm the presence of these organisms and compare their abundances across biocrust environments.

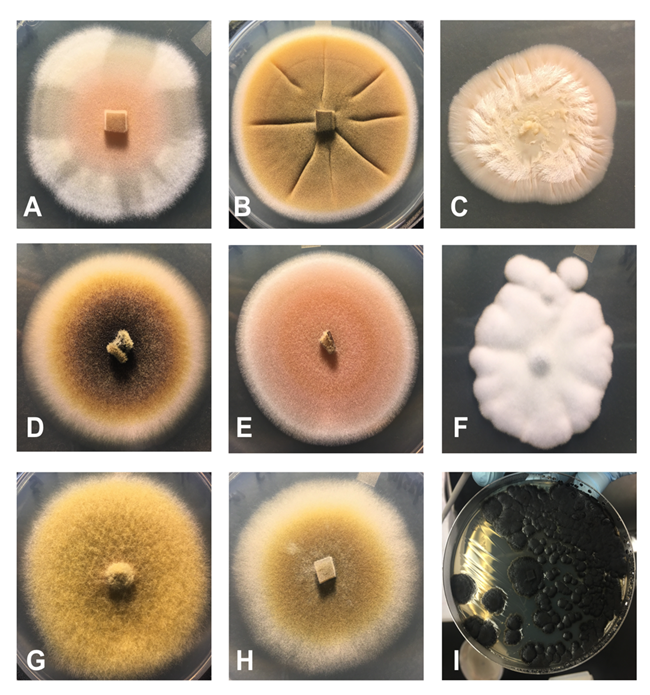
Figure 9. Depiction of a small sample of the variety of fungi isolated from the JTNP biocrusts by using a culture dependent method. The genera depicted include: A) Phoma sp., B) Didymella sp., C) Acremonium sp., D) Didymella sp., E) Aspergillus sp., F) Aspergillus sp., G) Alternaria sp., H) Phoma sp., I) Knufia sp..

Traditional culture dependent methods to isolate fungi generally use a nutrient rich media and are kept at room temperature. Because JTNP represents an extremely dry and cyclically hot environment, we experimented to find optimal growth conditions that might favor the more extremophilic species. We attempted growing the fungi in a range of temperatures, salt concentrations, and pH; we were successful in isolating fungi in the phyla Ascomycota and Basidiomycota with a range of growth rates (Figure 9). Examples of the fungal species we have brought into culture from biocrusts are Phoma sp., Didymella sp., Ustilaginales sp., Didymella sp., Aspergillus sp., Alternaria sp., and Knufia sp. Several of these fungal species match high abundance fungal gene markers that we identified from our culture independent amplicon sequencing of DNA from biocrust collected in the field. Using these starting cultures, we can test physiology, enzyme and biochemical properties, and interactions with algae and bacteria to better understand the roles these fungi play in the ecosystems.

Conclusion

We are only in the beginning stages of exploring the microbial diversity of biocrusts at JTNP. Based on the limited research that has been done in the park to date, we know that these microbial communities are very diverse and likely harbor many new species to science across all microbial lineages. In addition to knowing very little about the biological diversity found in these communities, we know even less about the specific adaptations of these microbes or the synergistic roles they play to contribute to ecosystem functions. Culture dependent and independent methods can both yield valuable information in the quest for more information regarding microbial diversity and the basic biology/ecology of these microorganisms. Culture dependent methods enable detailed studies of the biology of cyanobacteria, eukaryotic algae, and fungi found in these arid lands. However, culture dependent approaches are limited to the subset of organisms that can grow on culture media, therefore research that only focuses on these may miss a sizeable fraction of the actual microorganisms living in the soil. New sequencing technologies allow culture independent evaluation of microbial community diversity. Using NGS, we can produce a broader sampling of the microbial community diversity than is possible in the culture dependent approach. For the first time, additional abundant, but unculturable species, can be documented as part of the biocrust microbial community. Before we can hope to understand the function and processes that dominate these biocrusts, we must first document and identify the diversity present. Only then we can begin to quantify or explore how these microorganisms might contribute to ecosystem functions and/or how they respond to different environmental conditions. Finally, a better understanding of the microbial community can be used to develop management and monitoring strategies to assess the health of desert ecosystems and therefore to develop bioremediation strategies, such as the addition of missing community members. Overall, understanding the interactions and diversity of microbes that support biocrust formation and persistence are key aspects of desert land conservation

Future Research Directions

Our research shows that biocrusts are made up of very complex and unique microbial communities and we have just started to reveal the secret of these communities. Although eukaryotic algae, cyanobacteria, bacteria, and fungi have been found inhabiting biocrusts, their interactions and ecosystem functions are still under investigations. As we learn more about these microorganisms, important species will be revealed along with their functions. However, matching their cooperating microbes and relationships are very challenging at this early stage, since a fraction of microorganisms cannot be isolated using current culture dependent method. By exploring microbial diversity while developing both culture dependent and independent method, microbial interactions experiment can be conducted in the near future and will show how these microorganisms help each other to build biocrust community. Lastly, focusing more on filamentous and mycorrhizal fungi may help us evaluate the connections between biocrust microbial communities and vascular plants in drylands which has already been recognized as the fungal loop hypothesis (Collins et al. 2008).

Acknowledgement

This research was supported by funds from: the USDA Agriculture Experimental Station at University of California, Riverside and NIFA Hatch project CA-R-PPA-5062-H to J.E.S.; the California Desert Research Fund at The Community Foundation awarded to N. Pietrasiak; and Robert Lee Graduate Student Research Grants awarded to Nuttapon Pombubpa and Nicole Pietrasiak. Primer sequences and arrayed barcodes were provided by Alfred P. Sloan Foundation Indoor Microbiome Project. We thank Joshua Tree National Park for permits to allow us to conduct research. We thank Aurapat Ngamnithiporn, Derreck Carter-House, and Sangsan Warakkagun for assistance with biocrust sampling and transportation. We would also like to thank all 3 reviewers for their substantial suggestions and comments. Nuttapon Pombubpa was supported by Royal Thai Government Scholarship.

References

• Bates, S.T. and Garcia-Pichel, F., 2009. A culture-independent study of free-living fungi in biological soil crusts of the Colorado Plateau: their diversity and relative contribution to microbial biomass. Environmental Microbiology, 11(1), pp.56-67.
• Belnap, J. and Gardner, J.S., 1993. Soil microstructure in soils of the Colorado Plateau: the role of the cyanobacterium Microcoleus vaginatus. The Great Basin Naturalist, pp.40-47.
• Belnap, J., Eldridge, D.J., Kaltenecker, J.H., Rosentreter, R., Williams, J. and Leonard, S., 2001. Biological soil crusts: ecology and management. US Department of the Interior, Bureau of Land Management. US Geological Survey, Technical Reference, 2, pp.1-110.

• Belnap, J., 2002. Nitrogen fixation in biological soil crusts from southeast Utah, USA. Biology and fertility of soils, 35(2), pp.128-135.

• Belnap, J., Weber, B. and Büdel, B., 2016. Biological soil crusts as an organizing principle in drylands. In Biological Soil Crusts: An Organizing Principle in Drylands. Springer, Cham, pp.3-13.

• Bohunická, M., Pietrasiak, N., Johansen, J.R., Gómez, E.B., Hauer, T., Gaysina, L.A. and Lukešová, A., 2015. Roholtiella, gen. nov.(Nostocales, Cyanobacteria)—a tapering and branching cyanobacteria of the family Nostocaceae. Phytotaxa, 197(2), pp.84-103.

• Büdel, B., Dulić, T., Darienko, T., Rybalka, N. and Friedl, T., 2016. Cyanobacteria and algae of biological soil crusts. In Biological Soil Crusts: An Organizing Principle in Drylands. Springer, Cham, pp.55-80.

• Caporaso, J.G., Lauber, C.L., Walters, W.A., Berg-Lyons, D., Huntley, J., Fierer, N., Owens, S.M., Betley, J., Fraser, L., Bauer, M. and Gormley, N., 2012. Ultra-high-throughput microbial community analysis on the Illumina HiSeq and MiSeq platforms. The ISME journal, 6(8), p.1621.

• Clark, D.S., 1967. Comparison of pour and surface plate methods for determination of bacterial counts. Canadian journal of microbiology, 13(11), pp.1409-1412.

• Collins, S.L., Sinsabaugh, R.L., Crenshaw, C., Green, L., Porras-Alfaro, A., Stursova, M. and Zeglin, L.H., 2008. Pulse dynamics and microbial processes in aridland ecosystems. Journal of Ecology, 96(3), pp.413-420.
• Flechtner, V.R., Pietrasiak, N. and Lewis, L.A., 2013. Newly revealed diversity of green microalgae from wilderness areas of Joshua Tree National Park (JTNP). Monographs of the Western North American Naturalist, 6(1), pp.43-63.
• Fučíková, K., Flechtner, V.R. and Lewis, L.A., 2013. Revision of the genus Bracteacoccus Tereg (Chlorophyceae, Chlorophyta) based on a phylogenetic approach. Nova Hedwigia, 96(1-2), pp.15-59.
• Fučíková, K., Lewis, P.O. and Lewis, L.A., 2014. Putting incertae sedis taxa in their place: a proposal for ten new families and three new genera in Sphaeropleales (Chlorophyceae, Chlorophyta). Journal of phycology, 50(1), pp.14-25.
• Graham, L.E. Wilcox, L.W., Graham, J. 2009. Algae. 2nd ed. San Francisco: Benjamin Cummings.
• Hu, C., Liu, Y., Song, L. and Zhang, D., 2002. Effect of desert soil algae on the stabilization of fine sands. Journal of Applied Phycology, 14(4), pp.281-292.
• Maier, S., Muggia, L., Kuske, C.R. and Grube, M., 2016. Bacteria and Non-lichenized Fungi Within Biological Soil Crusts. In Biological Soil Crusts: An Organizing Principle in Drylands. Springer, Cham, pp.81-100.
• Maier, S., Tamm, A., Wu, D., Caesar, J., Grube, M. and Weber, B., 2018. Photoautotrophic organisms control microbial abundance, diversity, and physiology in different types of biological soil crusts. The ISME journal, p.1.
• Mühlsteinová, R., Johansen, J.R., Pietrasiak, N., Martin, M.P., Osorio-Santos, K. and Warren, S.D., 2014. Polyphasic characterization of Trichocoleus desertorum sp. nov. (Pseudanabaenales, Cyanobacteria) from desert soils and phylogenetic placement of the genus Trichocoleus. Phytotaxa, 163(5), pp.241-261.
• Nilsson, R.H., Tedersoo, L., Ryberg, M., Kristiansson, E., Hartmann, M., Unterseher, M., Porter, T.M., Bengtsson-Palme, J., Walker, D.M., De Sousa, F. and Gamper, H.A., 2015. A comprehensive, automatically updated fungal ITS sequence dataset for reference-based chimera control in environmental sequencing efforts. Microbes and Environments, 30(2), pp.145-150.
• Ondov, B.D., Bergman, N.H. and Phillippy, A.M., 2011. Interactive metagenomic visualization in a Web browser. BMC bioinformatics, 12(1), p.385.
• Osorio-Santos, K., Pietrasiak, N., Bohunická, M., Miscoe, L.H., Kováčik, L., Martin, M.P. and Johansen, J.R., 2014. Seven new species of Oculatella (Pseudanabaenales, Cyanobacteria): taxonomically recognizing cryptic diversification. European Journal of Phycology, 49(4), pp.450-470.
• Pietrasiak, N., Johansen, J.R., LaDoux, T. and Graham, R.C., 2011a. Comparison of disturbance impacts to and spatial distribution of biological soil crusts in the Little San Bernardino Mountains of Joshua Tree National Park, California. Western North American Naturalist, 71(4), pp.539-552.
• Pietrasiak, N., Johansen, J.R. and Drenovsky, R.E., 2011b. Geologic composition influences distribution of microbiotic crusts in the Mojave and Colorado Deserts at the regional scale. Soil Biology and Biochemistry, 43(5), pp.967-974.
• Pietrasiak, N., Regus, J.U., Johansen, J.R., Lam, D., Sachs, J.L. and Santiago, L.S., 2013. Biological soil crust community types differ in key ecological functions. Soil Biology and Biochemistry, 65, pp.168-171.
• Pietrasiak, N., Mühlsteinová, R., Siegesmund, M.A. and Johansen, J.R., 2014. Phylogenetic placement of Symplocastrum (Phormidiaceae, Cyanophyceae) with a new combination S. californicum and two new species: S. flechtnerae and S. torsivum. Phycologia, 53(6), pp.529-541.
• Řeháková, K., Johansen, J.R., Casamatta, D.A., Xuesong, L. and Vincent, J., 2007. Morphological and molecular characterization of selected desert soil cyanobacteria: three species new to science including Mojavia pulchra gen. et sp. nov. Phycologia, 46(5), pp.481-502.
• Smith, D.P. and Peay, K.G., 2014. Sequence depth, not PCR replication, improves ecological inference from next generation DNA sequencing. PloS one, 9(2), p.e90234.
• Steven, B., Yeager, C., Belnap, J. and Kuske, C.R., 2014. Common and distinguishing features of the bacterial and fungal communities in biological soil crusts and shrub root zone soils. Soil Biology and Biochemistry, 69, pp.302-312.
• Steven, B., Hesse, C., Gallegos-Graves, L.V., Belnap, J. and Kuske, C.R., 2015. Fungal diversity in biological soil crusts of the Colorado plateau. In Proc 12th Biennial Conf Science Management Colorado Plateau.
• Walters, W., Hyde, E.R., Berg-Lyons, D., Ackermann, G., Humphrey, G., Parada, A., Gilbert, J.A., Jansson, J.K., Caporaso, J.G., Fuhrman, J.A. and Apprill, A., 2016. Improved bacterial 16S rRNA gene (V4 and V4-5) and fungal internal transcribed spacer marker gene primers for microbial community surveys. Msystems, 1(1), pp.e00009-15.
• Weber, B., Belnap, J. and Büdel, B., 2016. Synthesis on Biological Soil Crust Research. In Biological Soil Crusts: An Organizing Principle in Drylands. Springer, Cham, pp.527-534.

Biography

Nuttapon (Nat) Pombubpa received his Bachelor’s degree with a double major in Molecular and Cellular Developmental Biology and Ecology and Evolutionary Biology from the University of Colorado Boulder in 2015. Then, he joined the Department of Microbiology and Plant Pathology at the University of California Riverside in Fall 2015, working under the supervision of Professor Jason E. Stajich. He is currently a Ph.D. candidate with research focuses on biological soil crusts (biocrusts), desert fungal diversity, and microbiome. He received Robert Lee Graduate Student Research Grant award from Joshua Tree National Park to work on using next generation amplicon sequencing to explore the composition of microbial communities and to investigate spatial and temporal patterns on biocrust microbiome in Joshua Tree National Park.